Chemical Effects of Current
Current can produce or speed up chemical change, this ability of current is called chemical effect (shown by dc not by ac).
Electrolytes: The liquids which allows the current to pass through them and also dissociates into ions on passing current through them are called electrolytes e.g. solutions of salts, acids and bases in water, etc.
Those liquids which do not allow current to pass through them are called insulators (e.g. vegetable oils, distilled water etc.)
Solutions of cane sugar, glycerin, alcohol etc. are examples of non-electrolytes.
Electrolysis: The process of decomposition of electrolyte solution into ions on passing the current through it is called electrolysis.
Practical applications of electrolysis are Electrotyping, extraction of metals from the ores, Purification of metals, Manufacture of chemicals, Production of O2 and H2, Medical applications and electroplating.
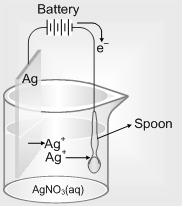
Electroplating: It is a process of depositing a thin layer of one metal over another metal by the method of electrolysis. The articles of cheap metals are coated with precious metals like silver and gold to make their look more attractive. The article to be electroplated is made the cathode and the metal to be deposited is made the anode. A soluble salt of the precious metal is taken as the electrolyte. (If gold is to be coated then auric chloride is used as electrolyte).
Solved example 1: In a copper voltameter experiment, current is decreased to one-fourth of the initial value but it is passed for four times the earlier duration. Amount of copper deposited will be
(A) Same (B) One-fourth the previous value
(C) Four times the previous value (D) of the previous value
Solution: (A) In the first case, Zit = m
In the second case, Z × i/4 × 4t = m.
Solved example 2: Two electrolytic cells containing CuSO4 and AgNO3 respectively are connected in series and a current is passed through them until 1 mg of copper is deposited in the first cell. The amount of silver deposited in the second cell during this time is approximately
(A) 1.7 mg (B) 3.4 mg (C) 5.1 mg (D) 6.8 mg
Solution: (B) m1/m2 = E1/E2 (By faraday law for same current and time)
Where E1 and E2 are the chemical equivalents and m1 and m2 are the masses of copper and silver respectively.
E = Atomic weight/Valency . E1 = 63.57/2 = 31.79 and Ez = 107.88/1 = 107.88
∴ 1mg/mz = 31.79/107.88 ⇒ mz = 107.88/31.79 mg = 3.4 mg.
Email Based Homework Assignment Help in Chemical Effects of Current
Transtutors is the best place to get answers to all your doubts regarding chemical effects of current, electrolytes, electrolysis, electroplating, voltameter with solved examples. You can submit your school, college or university level homework or assignment to us and we will make sure that you get the answers you need which are timely and also cost effective. Our tutors are available round the clock to help you out in any way with heating and chemical effects of current.Live Online Tutor Help for Chemical Effects of Current
Transtutors has a vast panel of experienced physics tutors who specialize in chemical effects of current and can explain the different concepts to you effectively. You can also interact directly with our physics tutors for a one to one session and get answers to all your problems in your school, college or university level heating and chemical effects of current homework. Our tutors will make sure that you achieve the highest grades for your physics assignments.Basic Motor Theory
Introduction
It has been said that if the Ancient Romans, with their advanced civilization and knowledge of the sciences, had been able to develop a steam motor, the course of history would have been much different. The development of the electric motor in modern times has indicated the truth in this theory. The development of the electric motor has given us the most efficient and effective means to do work known to man. Because of the electric motor we have been able to greatly reduce the painstaking toil of man's survival and have been able to build a civilization which is now reaching to the stars. The electric motor is a simple device in principle. It converts electric energy into mechanical energy. Over the years, electric motors have changed substantially in design, however the basic principles have remained the same. In this section of the Action Guide we will discuss these basic motor principles. We will discuss the phenomena of magnetism, AC current and basic motor operation.Magnetism
Now, before we discuss basic motor operation a short review of magnetism might be helpful to many of us. We all know that a permanent magnet will attract and hold metal objects when the object is near or in contact with the magnet. The permanent magnet is able to do this because of its inherent magnetic force which is referred to as a "magnetic field". In Figure 1 , the magnetic field of two permanent magnets are represented by "lines of flux". These lines of flux help us to visualize the magnetic field of any magnet even though they only represent an invisible phenomena. The number of lines of flux vary from one magnetic field to another. The stronger the magnetic field, the greater the number of lines of flux which are drawn to represent the magnetic field. The lines of flux are drawn with a direction indicated since we should visualize these lines and the magnetic field they represent as having a distinct movement from a N-pole to a S-pole as shown in Figure 1. Another but similar type of magnetic field is produced around an electrical conductor when an electric current is passed through the conductor as shown in Figure 2-a. These lines of flux define the magnetic field and are in the form of concentric circles around the wire. Some of you may remember the old "Left Hand Rule" as shown in Figure 2-b. The rule states that if you point the thumb of your left hand in the direction of the current, your fingers will point in the direction of the magnetic field.
Figure 1 - The lines of flux of a magnetic field travel from the N-pole to the S-pole.

Figure 2 - The flow of electrical current in a conductor sets up concentric lines of magnetic flux around the conductor.
 | Figure 3 - The magnetic lines around a current carrying conductor leave from the N-pole and re-enter at the S-pole. |

Figure 4 - The poles of an electro-magnetic coil change when the direction of current flow changes.
Magnetic Propulsion Within A Motor
The basic principle of all motors can easily be shown using two electromagnets and a permanent magnet. Current is passed through coil no. 1 in such a direction that a north pole is established and through coil no. 2 in such a direction that a south pole is established. A permanent magnet with a north and south pole is the moving part of this simple motor. In Figure 5-a the north pole of the permanent magnet is opposite the north pole of the electromagnet. Similarly, the south poles are opposite each other. Like magnetic poles repel each other, causing the movable permanent magnet to begin to turn. After it turns part way around, the force of attraction between the unlike poles becomes strong enough to keep the permanent magnet rotating. The rotating magnet continues to turn until the unlike poles are lined up. At this point the rotor would normally stop because of the attraction between the unlike poles. (Figure 5-b)

Figure 5
If, however, the direction of currents in the electromagnetic coils was suddenly reversed, thereby reversing the polarity of the two coils, then the poles would again be opposites and repel each other. (Figure 5-c). The movable permanent magnet would then continue to rotate. If the current direction in the electromagnetic coils was changed every time the magnet turned 180 degrees or halfway around,then the magnet would continue to rotate. This simple device is a motor in its simplest form. An actual motor is more complex than the simple device shown above, but the principle is the same.
AC Current
How is the current reversed in the coil so as to change the coils polarity, you ask. Well, as you probably know, the difference between DC and AC is that with DC the current flows in only one direction while with AC the direction of current flow changes periodically. In the case of common AC that is used throughout most of the United States, the current flow changes direction 120 times every second. This current is referred to as "60 cycle AC" or "60 Hertz AC" in honor of Mr. Hertz who first conceived the AC current concept. Another characteristic of current flow is that it can vary in quantity. We can have a 5 amp, 10 amp or 100 amp flow for instance. With pure DC, this means that the current flow is actually 5,10, or 100 amps on a continuous basis. We can visualize this on a simple time-current graph by a straight line as shown in Figure 6.
Figure 6 - Visualization of DC
But with AC it is different. As you can well imagine, it would be rather difficult for the current to be flowing at say 100 amps in a positive direction one moment and then at the next moment be flowing at an equal intensity in the negative direction. Instead, as the current is getting ready to change directions, it first tapers off until it reaches zero flow and then gradually builds up in the other direction. See Figure 7. Note that the maximum current flow (the peaks of the line) in each direction is more than the specified value (100 amps in this case). Therefore, the specified value is given as an average. It is actually called a "root mean square" value, but don't worry about remembering this because it is of no importance to us at this time. What is important in our study of motors, is to realize that the strength of the magnetic field produced by an AC electro-magnetic coil increases and decreases with the increase and decrease of this alternating current flow.

Figure 7 - Visualization of AC.
Basic AC Motor Operation
An AC motor has two basic electrical parts: a "stator" and a "rotor" as shown in Figure 8. The stator is in the stationary electrical component. It consists of a group of individual electro-magnets arranged in such a way that they form a hollow cylinder, with one pole of each magnet facing toward the center of the group. The term, "stator" is derived from the word stationary. The stator then is the stationary part of the motor. The rotor is the rotating electrical component. It also consists of a group of electro-magnets arranged around a cylinder, with the poles facing toward the stator poles. The rotor, obviously, is located inside the stator and is mounted on the motor's shaft. The term "rotor" is derived from the word rotating. The rotor then is the rotating part of the motor. The objective of these motor components is to make the rotor rotate which in turn will rotate the motor shaft. This rotation will occur because of the previously discussed magnetic phenomenon that unlike magnetic poles attract each other and like poles repel. If we progressively change the polarity of the stator poles in such a way that their combined magnetic field rotates, then the rotor will follow and rotate with the magnetic field of the stator.

Figure 8 - Basic electrical components of an AC motor.
This "rotating magnetic fields of the stator can be better understood by examining Figure 9. As shown, the stator has six magnetic poles and the rotor has two poles. At time 1, stator poles A-1 and C-2 are north poles and the opposite poles, A-2 and C-1, are south poles. The S-pole of the rotor is attracted by the two N-poles of the stator and the N-pole of the rotor is attracted by the two south poles of the stator. At time 2, the polarity of the stator poles is changed so that now C-2 and B-1 and N-poles and C-1 and B-2 are S-poles. The rotor then is forced to rotate 60 degrees to line up with the stator poles as shown. At time 3, B-1 and A-2 are N. At time 4, A-2 and C-1 are N. As each change is made, the poles of the rotor are attracted by the opposite poles on the stator. Thus, as the magnetic field of the stator rotates, the rotor is forced to rotate with it.

Figure 9 - The rotating magnetic field of an AC motor.
One way to produce a rotating magnetic field in the stator of an AC motor is to use a three-phase power supply for the stator coils. What, you may ask, is three-phase power? The answer to that question can be better understood if we first examine single-phase power. Figure 7 is the visualization of single-phase power. The associated AC generator is producing just one flow of electrical current whose direction and intensity varies as indicated by the single solid line on the graph. From time 0 to time 3, current is flowing in the conductor in the positive direction. From time 3 to time 6, current is flowing in the negative. At any one time, the current is only flowing in one direction. But some generators produce three separate current flows (phases) all superimposed on the same circuit. This is referred to as three-phase power. At any one instant, however, the direction and intensity of each separate current flow are not the same as the other phases. This is illustrated in Figure 10. The three separate phases (current flows) are labeled A, B and C. At time 1, phase A is at zero amps, phase B is near its maximum amperage and flowing in the positive direction, and phase C is near to its maximum amperage but flowing in the negative direction. At time 2, the amperage of phase A is increasing and flow is positive, the amperage of phase B is decreasing and its flow is still negative, and phase C has dropped to zero amps. A complete cycle (from zero to maximum in one direction, to zero and to maximum in the other direction, and back to zero) takes one complete revolution of the generator. Therefore, a complete cycle, is said to have 360 electrical degrees. In examining Figure 10, we see that each phase is displaced 120 degrees from the other two phases. Therefore, we say they are 120 degrees out of phase.

Figure 10 - The pattern of the separate phases of three-phase power.
To produce a rotating magnetic field in the stator of a three-phase AC motor, all that needs to be done is wind the stator coils properly and connect the power supply leads correctly. The connection for a 6 pole stator is shown in Figure 11. Each phase of the three-phase power supply is connected to opposite poles and the associated coils are wound in the same direction. As you will recall from Figure 4, the polarity of the poles of an electro-magnet are determined by the direction of the current flow through the coil. Therefore, if two opposite stator electro-magnets are wound in the same direction, the polarity of the facing poles must be opposite. Therefore, when pole A1 is N, pole A2 is S. When pole B1 is N, B2 is S and so forth.

Figure 11 - Method of connecting three-phase power to a six-pole stator.
Figure 12 shows how the rotating magnetic field is produced. At time1, the current flow in the phase "A" poles is positive and pole A-1 is N. The current flow in the phase "C" poles is negative, making C-2 a N-pole and C-1 is S. There is no current flow in phase "B", so these poles are not magnetized. At time 2, the phases have shifted 60 degrees, making poles C-2 and B-1 both N and C-1 and B-2 both S. Thus, as the phases shift their current flow, the resultant N and S poles move clockwise around the stator, producing a rotating magnetic field. The rotor acts like a bar magnet, being pulled along by the rotating magnetic field.

Figure 12 - How three-phase power produces a rotating magnetic field.
Up to this point not much has been said about the rotor. In the previous examples, it has been assumed the rotor poles were wound with coils, just as the stator poles, and supplied with DC to create fixed polarity poles. This, by the way, is exactly how a synchronous AC motor works. However, most AC motors being used today are not synchronous motors. Instead, so-called "induction" motors are the workhorses of industry. So how is an induction motor different? The big difference is the manner in which current is supplied to the rotor. This is no external power supply. As you might imagine from the motor's name, an induction technique is used instead. Induction is another characteristic of magnetism. It is a natural phenomena which occurs when a conductor (aluminum bars in the case of a rotor, see Figure 13) is moved through an existing magnetic field or when a magnetic field is moved past a conductor. In either case, the relative motion of the two causes an electric current to flow in the conductor. This is referred to as "induced" current flow. In other words, in an induction motor the current flow in the rotor is not caused by any direct connection of the conductors to a voltage source, but rather by the influence of the rotor conductors cutting across the lines of flux produced by the stator magnetic fields. The induced current which is produced in the rotor results in a magnetic field around the rotor conductors as shown in Figure 14. This magnetic field around each rotor conductor will cause each rotor conductor to act like the permanent magnet in the Figure 9 example. As the magnetic field of the stator rotates, due to the effect of the three-phase AC power supply, the induced magnetic field of the rotor will be attracted and will follow the rotation. The rotor is connected to the motor shaft, so the shaft will rotate and drive the connection load. That's how a motor works! Simple, was it not?

Figure 13 - Construction of an AC induction motor's rotor.

Figure 14 - How voltage is induced in the rotor, resulting in current flow in the rotor conductors.
DC Motor Theory
Preface
The intent of this paper is to provide one with an understanding of DC Motors in order that they can be applied with confidence. This paper contains basic information and specific information that applies to Reliance Medium HP and Large HP DC Motors. Due to the nature of Baldor Systems business, emphasis has been placed on the Large DC motor product line.Section 1: Dynamo Development
The first generators and motors were called dynamos or dynamoelertric machines. Dynamo is from the Greek word dynamis which means power. Webster defines dynamoelectric as "relating to the conversion of mechanical energy into electrical energy or vice versa". The word motor is from the Latin word motus which means one that imparts motion or prime mover. The dynamo was the result of the efforts of several people, in different countries, in the mid-nineteenth century, to make electricity work for them.Definitions
| Dynamo: | From the Greek word dynamis, which means power |
| Dynamoelectric: | Relating to the conversion by induction of mechanical energy into electrical energy or vice versa |
| Dynamoelectric machine: | A dynamo or generator |
| Motor: | From the Latin word motus, one that imparts motion, prime mover. A device that changes electrical energy into mechanical energy. |
| Generator: | A device that changes mechanical energy into electrical energy. Although the terms AC and DC generator are in common usage, a generator is normally considered to be a device that provides DC current. |
| Alternator: | A device that changes mechanical energy into an alternating current electrical energy, an AC generator. |
Landmarks Of Electric Motor Development
| 1820 The discovery of electromagnetism Hans Christian Oersted, Danish |
| 1827 The statement of the law of electric conduction, Ohm's law George S. Ohm, German |
| 1830 The discovery of electromagnetic induction Joseph Henry, American |
| 1831 The discovery of electromagnetic induction Michael Faraday, English |
The first practical dynamo, about 1867
Section 2: Electric Motor And Generator Basics
Electrodynamic Principles
Faraday's LawIn order that current can be obtained from an electric circuit, an electromotive force (voltage) must be established and maintained between the two ends of the circuit. This electromotive force may be established in several ways, one of which is by means of an electromagnetic generator.
Michael Faraday discovered that an electric potential can be established between the ends of a conductor in the following three ways:
- By a conductor moving or cutting across a stationary magnetic field. (DC Generator)
- By a moving magnetic field cutting across a stationary conductor. (AC Generator)
- By a change in the number of magnetic lines enclosed by a stationary loop or coil. (Transformer)
Faraday's law states that, "the EMF (electromotive force) induced between the ends of a loop or coil is proportional to the rate of change of magnetic flux enclosed by the coil; or the EMF induced between the ends of a bar conductor is proportional to the time rate at which magnetic flux is cut by the conductor."
This law emphasizes rate of change or rate or flux cutting rather than density or extent of magnetic field.
Lenz's Law
Lenz's Law states that, "A change in the magnetic flux passing through or linking with, a loop or coil causes EMF to be induced in a direction to oppose any change in circuit conditions, this opposition being produced magnetically when current flows in response to the induced EMF."
Whenever there is a change in current in a magnetizing coil, which works to change the flux in the coil, a voltage is induced which tends to prevent the change. Thus, if we attempt to diminish the current flowing in a magnetizing coil, a voltage will be developed that will tend to keep the current unchanged. Likewise, if we attempt to establish a current in a magnetizing coil, a voltage will be developed that will tend to keep the current from increasing.
Generator Basic Principles
Energy ConversionTo produce voltage, it is necessary to move a conductor through a magnetic field as stated above. Mechanical energy is required to provide motion to this conductor. With the field energy remaining constant, the conductor is changing mechanical energy into electrical energy.
Voltage Generation
There is a definite relationship between the direction of the magnetic flux, the direction of motion of the conductor and the direction of the induced EMF. Figure 1 shows the motion of the conductor perpendicular to the magnetic field. The voltage and current output are perpendicular to both the motion of the conductor and the magnetic field.
 | Figure 1. Voltage Generation |
Applying this rule, one can see that the current will reverse if the motion of the conductor changes from down to up. This is true even though the magnetic field does not change position. Therefore, the rotating coil in Figure 2 will produce a voltage which is continually changing direction.
 | Figure 2. Revolving Coil in a Magnetic Field
|
Although the flux is maximum at positions AB and BA and zero at positions CD and DC, the induced EMF will be maximum at positions CD and DC and zero at positions AB and BA. This is true because the EMF depends upon the rate of change of flux or rate of cutting flux lines and not upon the quantity enclosed.
If the coil in Figure 2 were rotated at a constant speed in a uniform magnetic field, a sine wave of voltage would be obtained. This is shown in Figure 3 where both the amount of flux enclosed and the EMF induced are plotted against time.
 | Figure 3. Voltage Sine Wave Produced by rotation of a coil at constant speed in a uniform magnetic field. |
The EMF at any instant of time is proportional to the number of turns in the coil times rate of change of flux. The C.G.S. (centimeter gram second) unit of EMF known as the abvolt is defined as that value induced, in a coil of one turn, when the flux linking with the coil is changing at the rate of one line or Maxwell per second; or as that value induced when magnetic flux is being cut by the conductor at the rate of one line per second. A volt is equal to 108 abvolts or an abvolt is equal to 10-8 volts. Therefore, the instantaneous value of voltage is expressed as:
e = N x (d  / dt) x 10-8 / dt) x 10-8 |
| e = voltage | |
| N = the number of turns | |
d  / dt = the rate of change of flux / dt = the rate of change of flux |
E = N B  v sin v sin  x 10-8 x 10-8 |
| E = voltage | |
| N = number of turns | |
| B = flux density in lines per square inch | |
 = length of the conductor in inches = length of the conductor in inches | |
| v = velocity in inches per second | |
 = the angle between the conductor and flux field = the angle between the conductor and flux field |
 = 90° and sin
= 90° and sin  = 1. The equation then becomes:
= 1. The equation then becomes: E = N B  v x 10-8 v x 10-8 |
MOTOR BASIC PRINCIPLES
Energy ConversionAs stated above, mechanical energy is changed into electrical energy by movement of conductor through a magnetic field. The converse of this is also true. If electrical energy is supplied to a conductor lying normal to a magnetic field, resulting in current flow in the conductor, a mechanical force and thus mechanical energy will be produced.
Producing Mechanical Force
As in the generator, the motor has a definite relationship between the direction of the magnetic flux, the direction of motion of the conductor or force, and the direction of the applied voltage or current.
Since the motor is the reverse of the generator, Fleming's left hand rule can be used. If the thumb and first two fingers of the left hand are extended at right angles to one another, the thumb will indicate the direction of motion, the forefinger will indicate the direction of the magnetic field, and the middle finger will indicate the direction of current. In either the motor or generator, if the directions of any two factors are known, the third can be easily determined.
Value of Mechanical Force
The force exerted upon a current carrying conductor is dependent upon the density of the magnetic field, the length of conductor, and the value of current flowing in the conductor. Assuming that the conductor is located at right angles to the magnetic field, the force developed can be expressed as follows:
F = (B  I) / 10 I) / 10 |
| F = force in dynes | |
| B = flux density in lines per square centimeter | |
 = length of the conductor in centimeters = length of the conductor in centimeters | |
| I = current in amperes. |
Sample Calculations
GeneratorGiven:
| N = 60 turns | |
| B = 40,000 lines per square inch | |
 = 3.0 inches = 3.0 inches | |
| v = 600 inches per second |
| E = voltage | ||
| E = 60 x 40,000 x 3 x 600 x 10-8 = 43.2 volts |
Given:
| B = 6,000 lines per square centimeter | |
 = 10 Centimeters = 10 Centimeters | |
| I = 50 amps |
| F = force | |
| F = (6,000 x 10 x 50) / 10 = 300,000 dynes | |
| Newtons = Pounds x 4.44823 | |
| Dynes = Newtons x 100,000 |
DC Machines, Principles Of Operation
GeneratorIn a generator, moving a conductor through a stationary magnetic field generates voltage. If a coil is rotated through a magnetic field as shown in Figure 4, an alternating voltage will be produced. To make this voltage available to a stationary external circuit, two slip rings and brushes must be provided. For the external circuit to produce DC voltage, it is necessary to reverse the polarity of the external leads at the same time the voltage in the coil is reversed. This is accomplished by segmenting a slip ring to form what is called a commutator. An elementary two segment commutator is illustrated in Figure 5. This single coil, two piece commutator will yield an unidirectional but pulsating voltage as shown in Figure 6. However, when a large number of commutator segments or bars is used, the resulting voltage will be more uniform as shown in Figure 7.
 | Figure 4. Brushes and slip rings provide AC voltage |
 | Figure 5. Brushes and Commutator provides DC voltage |
 Figure 6.
Figure 6. Unidirectional, Pulsating Voltage
 Figure 7.
Figure 7. Uniform DC Voltage
As stated above, the generated voltage in a single conductor is:
E = N B  v x 10-8 v x 10-8 |
| B = flux density in lines per square inch | |
 = length of the conductor in inches = length of the conductor in inches | |
| v = velocity in inches per second |
E = (Z / paths) x  x poles x (rpm / 60) x 10-8 x poles x (rpm / 60) x 10-8 |
| Z = total number of conductors | |
 = flux per pole in lines = flux per pole in lines |
E = K1  S S |
 = flux per pole = flux per pole | |
| S = speed in rpm | |
| K1 = all other factors |
As stated previously, if current is supplied to a conductor in a magnetic field, a force will be produced. The force developed in a single conductor is:
F = (B  I) / 10 I) / 10 |
| F = force in dynes | |
| B = flux density in lines per square centimeter | |
 = length of the conductor in centimeters = length of the conductor in centimeters | |
| I = current in amperes |
T = 11.73 x (Z / paths) x  x poles x IA x 10-10 x poles x IA x 10-10 |
| T = torque in ft-lb | |
| Z = total number of conductors | |
 = flux per pole in lines = flux per pole in lines | |
| I = current in amperes |
T = K2  IA IA |
 = flux per pole in lines = flux per pole in lines | |
| IA = current in amperes | |
| K2 = all other factors |
The horsepower output of any motor can be expressed as:
| HP = T x N / C |
| T = output torque in ft-lb | |
| N = speed in rpm | |
| C = the constant 5252 |
DC General Construction
A typical DC generator or motor usually consists of: An armature core, an air gap, poles, and a yoke which form the magnetic circuit; an armature winding, a field winding, brushes and a commutator which form the electric circuit; and a frame, end bells, bearings, brush supports and a shaft which provide the mechanical support. See figure 8. Figure 8.
Figure 8. Four Pole DC Motor
Armature Core or Stack
The armature stack is made up thin magnetic steel laminations stamped from sheet steel with a blanking die. Slots are punched in the lamination with a slot die. Sometimes these two operations are done as one. The laminations are welded, riveted, bolted or bonded together.
Armature Winding
The armature winding is the winding, which fits in the armature slots and is eventually connected to the commutator. It either generates or receives the voltage depending on whether the unit is a generator or motor. The armature winding usually consists of copper wire, either round or rectangular and is insulated from the armature stack.
Field Poles
The pole cores can be made from solid steel castings or from laminations. At the air gap, the pole usually fans out into what is known as a pole head or pole shoe. This is done to reduce the reluctance of the air gap. Normally the field coils are formed and placed on the pole cores and then the whole assembly is mounted to the yoke.
Field Coils
The field coils are those windings, which are located on the poles and set up the magnetic fields in the machine. They also usually consist of copper wire are insulated from the poles. The field coils may be either shunt windings (in parallel with the armature winding) or series windings (in series with the armature winding) or a combination of both.
Yoke
The yoke is a circular steel ring, which supports the field, poles mechanically and provides the necessary magnetic path between the pole. The yoke can be solid or laminated. In many DC machines, the yoke also serves as the frame.
Commutator
The commutator is the mechanical rectifier, which changes the AC voltage of the rotating conductors to DC voltage. It consists of a number of segments normally equal to the number of slots. The segments or commutator bars are made of silver bearing copper and are separated from each other by mica insulation.
Brushes and Brush Holders
Brushes conduct the current from the commutator to the external circuit. There are many types of brushes. A brush holder is usually a metal box that is rectangular in shape. The brush holder has a spring that holds the brush in contact with the commutator. Each brush usually has a flexible copper shunt or pigtail, which extends to the lead wires. Often, the entire brush assembly is insulated from the frame and is made movable as a unit about the commutator to allow for adjustment.
Interpoles
Interpoles are similar to the main field poles and located on the yoke between the main field poles. They have windings in series with the armature winding. Interpoles have the function of reducing the armature reaction effect in the commutating zone. They eliminate the need to shift the brush assembly.
Frame, End Bells, Shaft, and Bearings
The frame and end bells are usually steel, aluminum or magnesium castings used to enclose and support the basic machine parts. The armature is mounted on a steel shaft, which is supported between two bearings. The bearings are either sleeve, ball or roller type. They are normally lubricated by grease or oil.
Back End, Front End
The load end of the motor is the Back End. The opposite load end, most often the commutator end, is the Front End of the motor.
Armature Windings
Gramme Ring WindingThe old Gramme Ring type winding, now obsolete, is shown in Figure 9 and its equivalent circuit in Figure 10. It can be seen that there are an equal number of voltage-generating conductors on each side of the armature and the conductor voltages are additive from bottom to top on each side. There are two paths between the positive and negative brushes and the voltage per path is the generated voltage of the machine. Each path provides half of the current output.
 | Figure 9. Two Pole Gramme Ring Winding |
 | Figure 10. Equivalent Circuit, Two Pole Gramme Ring Winding |
The Drum type winding is made of coils, one of which is illustrated in Figure 11. The straight portions of the coil are the parts rotating through the magnetic field in which the voltage is induced. Therefore, each single coil has two conductors. This has the advantage over the Gramme Ring winding where only one side of each coil is used as an active conductor. There are two classes of drum windings depending upon how the coils are connected to the commutator.
 | Figure 11. Drum Type Winding Coil |
When the end connections of the coils are brought to adjacent bars as shown in Figure 12, a lap or parallel winding is formed. In this type winding, there are as many paths through the armature as there are poles on the machine. Therefore, to obtain full use of this type winding, there must be as many brushes as there are poles, alternate brushes being positive and negative. Any winding can be illustrated in one of two forms, the circular form or the development form. A simplex lap winding is shown in Figure 13 (circular form) and Figure 14 (development form.) In this particular circular form, the flux cutting portions of the conductors are shown as straight lines radiating from the center and are numbered for convenience in connecting them to the commutator which is in the center of the diagram. The outermost connecting lines represent the end connections on the back of the armature and the inner connecting lines represent the connections on the front or commutator end of the armature. The development form of winding represents the armature as if it were split open and rolled out flat. It is somewhat simpler to understand but the continuity of the winding is broken. The lap winding is best suited for low voltage, high current ratings because of the number of parallel paths.
 | Figure 12. Lap Winding connected to commutator bars |
 | Figure 13. Simplex Lap Winding, Circular Form |
 Figure 14.
Figure 14. Simplex Lap Winding, Development Form
Wave Winding
When the end connections of the coils are spread apart as shown in Figure 15 a wave or series winding is formed. In a wave winding there are only two paths regardless of the number of poles. Therefore, this type winding requires only two brushes but can use as many brushes as poles. The simplex wave winding in Figure 16 (circular) and Figure 17 (development) shows that the connections to the armature do not lap back toward the coil but progress forward. The coil voltages are cumulative but it is necessary to travel several times around the armature and to traverse half the total winding in order to trace the path between the positive and negative brush. The wave winding is best suited for high voltage low current ratings since it has only two paths.
 | Figure 15. Wave Winding connected to commutator bars |
 | Figure 16. Simplex Wave Winding, Circular Form |
 Figure 17.
Figure 17. Simplex Wave Winding, Development Form
Slots and Coils
The number and size of slots depend upon the generator or motor requirements. The slot has to be large enough to hold the correct number of conductors but at the same time, the tooth has to be large enough to pass the necessary magnetic flux. Normally, in a simple winding, there are as many coils as there are slots. This means that each slot contains two coil sides, one side of each coil being at the top of a slot and the other at the bottom of a slot. Each coil may consist of one or more turns depending on the applied or generated voltage of the unit. A typical arrangement of coil sides and slots is shown in Figure 18. Solid lines represent the front end connections to the commutator and dotted lines represent the back end connections.
Slot Pitch
Slot pitch refers to the number of slots spanned by each coil. For example, in Figure 18, the top of coil in slot 1 has its bottom in slot 4, therefore, the slot pitch is 1-4 or 3. Since the top of the coil is directly under the north pole and the bottom is directly under the south pole, the winding is known as a full pitch winding. In many cases, for various reasons, the pitch is reduced to less than full pitch. For example, if the coils in Figure 6 spanned 2 slots instead of three, the winding would become a two-thirds pitch winding.
 | Figure 18. Coil Sides in Armature Slots |
Field Windings
The field windings provide the excitation necessary to set up the magnetic fields in the machine. There are various types of field windings that can be used in the generator or motor circuit. In addition to the following field winding types, permanent magnet fields are used on some smaller DC products. See Figure 19 for winding types. | Shunt Wound - DC Operation Shunt wound motors, with the armature shunted across the field, offer relatively flat speed-torque characteristics. Combined with inherently controlled no-load speed, this provides good speed regulation over wide load ranges. While the starting torque is comparatively lower than the other DC winding types, shunt wound motors offer simplified control for reversing service. Typical Speed - Torque Curve |
 | Compound Wound - DC Operation Compound wound (stabilized shunt) motors utilize a field winding in series with the armature in addition to the shunt field to obtain a compromise in performance between a series and shunt type motor. This type offers a combination of good starting torque and speed stability. Standard compounding is about 12%. Heavier compounding of up to 40 to 50% can be supplied for special high starting torque applications, such as hoists and cranes. Typical Speed - Torque Curve |
 | Series Wound - DC Operation Series wound motors have the armature connected in series with the field. While it offers very high starting torque and good torque output per ampere, the series motor has poor speed regulation. Speed of DC series motors is generally limited to 5000 rpm and below. Series motors should be avoided in applications where they are likely to lose there load because of their tendency to "run away" under no-load conditions. These are generally used on crane and hoist applications. Typical Speed - Torque Curve |
 | Permanent Magnet - DC Operation Permanent magnet motors have no wound field and a conventional wound armature with commutator and brushes. This motor has excellent starting torques, with speed regulation not as good as compound motors. However, the speed regulation can be improved with various designs, with corresponding lower rated torques for a given frame. Because of permanent field, motor losses are less with better operating efficiencies. These motors can be dynamically braked and reversed at some low armature voltage (10%) but should not be plug reversed with full armature voltage. Reversing current can be no higher than the locked armature current. Typical Speed - Torque Curve |
Field Windings
Separately Excited Winding
When the field is connected to an external power source, it is a separately excited field.
Straight Shunt Winding
This winding is connected in parallel with the armature. Shunt windings usually consists of a large number of turns of small size wire. This is a good winding for reversing applications since it provides the same amount of torque in both directions. The torque/ current curve is non-linear above full load. Shunt wound motors often have a rising speed characteristic with increased load.
Series Winding
This winding is connected in series with the armature. A series winding usually consists of a small number of turns of large size wire. With this winding, the motor can produce high starting and overload torque. This design is not used for applications with light loads or no load conditions.
Compound Winding
This winding consists of a shunt winding and a series winding. This is also known as compound excitation. The series winding can be designed as a starting series only or as a start and run series.
Stabilized Shunt Winding
Like the compound winding, this winding consists of a shunt winding and a series winding. The series or stabilizing winding has a fewer number of turns than the series winding in a compound wound machine. A stabilizing winding is used to assures a speed droop with overload. It also adds to the torque in one direction of operation and subtracts from torque in the reverse direction of operation and in regeneration.
Shunt Compensated Winding
Shunt compensated motors have a shunt winding and a pole face series winding made up of large conductors placed in slots in the face of the main field poles. The direction of current in the compensating windings is the opposite of the current in the armature conductors passing under the poles. The flux produced by the compensating windings neutralizes the flux of the armature conductors passing under the poles so that distortion of air gap flux is minimized. Shunt compensated motors maintain constant or set speed well at all loads, no load through overload. Unlike the stabilized shunt winding, the pole face winding adds to torque in both the forward and reverse direction of rotation. Shunt compensated windings, due to cost and difficulty of construction, are provided on large motors only, usually 840 frames and larger.
Commutation
The maximum voltage from an armature winding can be obtained when the brushes are in contact with those conductors, which are midway between the poles. This will result in the greatest possible number of conductors cutting the magnetic lines in one direction between a positive and negative brush. This brush position is known as the no load neutral position of the brushes. The current in a given armature coil reverses in direction as the coil sides move from one pole to another of opposite polarity, whereas the function of the commutator is to keep the current unidirectional. This reversal of current is known as commutation. The commutator acts as a switch to keep the current flowing in one direction. However, the fast rate of change in direction of the current in any given coil induces an appreciable voltage in that coil which tends to keep the current flowing in the original direction. Therefore, the current reversal is delayed causing an accelerated rate of change near the end of the commutation period. This results in an arc if the reversal is not completed before the brush breaks contact with the coil involved. Any arcing is detrimental to the operation of the machine and must be counteracted.Armature Reaction
Since the armature conductors carry current they set up a magnetic field which distorts or opposes the main field. This is called armature reaction and is a function of the amount of load present. Figure 21 shows the MMF and flux wave shapes due to the armature reaction only; and Figure 22 shows the combined effect of both. It can be seen that armature reaction causes the flux to shift, thus tending to saturate one pole tip. If this effect is appreciable, it can be detrimental to the satisfactory performance of the machine. If severe enough, it may result in a flashover, which is the progressive arcing over successive bars until the arc extends from positive to negative brush, thus short circuiting the machine terminals.
 Figure 20.
Figure 20. MMF and Flux Wave Shape due to Main Field only
 Figure 21.
Figure 21. MMF and Flux Wave Shape due to Armature Reaction only
 Figure 22.
Figure 22. Flux Wave Shape, combined effect
Brush Shifting
One method of reducing the arcing due to non-linear commutation is to shift the brushes away from the geometrical neutral position. Then commutation will occur when the applicable coil is under the influence of a weak magnetic field that will generate a voltage in the coil, which opposes the induced voltage due to current change. Therefore, this new voltage will assist rather than hinder the current reversal. In a generator, it is necessary to shift the brushes forward in the direction of rotation for good commutation. This is true because the current flow through the conductors is in the same direction as the voltage and, it commutation is delayed until the coil sides are under the next pole, it will be assisted by the current reversing voltage. In a motor, it is necessary to shift the brushes against the direction of rotation because current flow is in opposition to the induced voltage. The amount of shift necessary depends on the load so a given shift will not be satisfactory for all loads. One effect of shifting brushes is that a demagnetization component of armature reaction is introduced. In other words, when the brushes are shifted, the armature reaction will not only distort the main field flux but it will also directly oppose the main field. This will result in a reduction of the field flux. Another effect is that if the brushes are shifted far enough, it is possible to reduce the number of effective turns because there will be voltages in opposition to each other between two brushes.
In generators the demagnetization component of armature reaction would be detrimental because there will be a decrease in generated voltage with increase in load. However, in a motor, the effect would be beneficial because the speed would tend to remain constant.
Interpoles
Another method to combat the induced voltage caused by current reversal is the use of interpoles. The interpoles are located at the geometric neutral points midway between the main poles and provide reversing magnetic field of proper strength and polarity. They eliminate the need for brush shifting and, because of this, the demagnetization effect of armature reaction is eliminated. The interpole must have sufficient strength to overcome the armature reaction and provide a reversing field, therefore, it is connected in series with the armature winding. When the armature current is increased in the same proportion. In a generator, the interpole must have the same polarity as the next pole in the direction of rotation while in a motor the interpole must have the same polarity as the last pole.
Generator Characteristics
No Load Saturation CurveA typical no load saturation curve is shown in Figure 23. This is similar to the magnetization curve mentioned previously except that it represents the entire magnetic circuit of a machine rather than one particular magnetic material. Also, it has generator output voltage plotted against field current rather than flux density against magnetizing force. This can be done since generator voltage is directly proportional to the field flux and the number of turns is fixed. There is a different saturation curve for each speed. The lower straight line portion of the curve represents the air gap because the magnetic parts are not saturated. When the magnetic parts start to saturate, the curve bends over until complete saturation is reached. Then the curve becomes a straight line again.
 Figure 23.
Figure 23. No Load Saturation Curve
 | Figure 23.1 No Load Saturation Curve |
 | Figure 23.2 No Load Saturation Curve |
Generator build up usually refers to the gradual rise in voltage at the armature terminals when the machine is self-excited and operated at normal speed. This is illustrated in Figure 25 by referring to the field resistance line which shows how the field current varies as field voltage is varied. The slope of this line is the field resistance at a constant temperature. The voltage rise starts with the residual magnetism of the field iron. This provides a small voltage output E1 that is fed back to the field as
 1.
1. 1 increases the flux providing a slightly larger voltage, E2 . E2 causes
1 increases the flux providing a slightly larger voltage, E2 . E2 causes  2 to flow. This process continues until the machine starts to saturate and stops at the point where the field resistance line intersects the saturation curve. If the speed of the machine is reduced so that the saturation curve becomes tangent to field resistance curve, the voltage will not build up. This is known as the critical speed. Also, at any given speed, if the field resistance is increased by addition of external resistance, a critical resistance can be reached.
2 to flow. This process continues until the machine starts to saturate and stops at the point where the field resistance line intersects the saturation curve. If the speed of the machine is reduced so that the saturation curve becomes tangent to field resistance curve, the voltage will not build up. This is known as the critical speed. Also, at any given speed, if the field resistance is increased by addition of external resistance, a critical resistance can be reached.  Figure 25.
Figure 25. DC Motor Curves
Voltage Output The voltage equation has been expressed as:
E = K1  S. S. |
V = E - Ia Ra - K1  S - Ia Ra S - Ia Ra |
| E = generated voltage | |
| Ia = armature current | |
| Ra = armature circuit resistance | |
| K1 = machine constants | |
 = flux per pole = flux per pole | |
| S = speed. |
The curve showing the relationship between output voltage and output current is known as the external characteristic. Shown in Figure 24 are the external characteristic curves for generators with various types of excitation. If a generator, which is separately excited, is driven at constant speed and has a fixed field current, the output voltage will decrease with increased load current as shown. This decrease is due to the armature resistance and armature reaction effects. If the field flux remained constant, the generated voltage would tend to remain constant and the output voltage would be equal to the generated voltage minus the IR drop of the armature circuit. However, the demagnetizing component of armature reactions tends to decrease the flux, thus adding an additional factor, which decreases the output voltage.
 Figure 24.
Figure 24. DC Generator Curves
In a shunt excited generator, it can be seen that the output voltage decreases faster than with separate excitation. This is due to the fact that, since the output voltage is reduced because of the armature reaction effect and armature IR drop, the field voltage is also reduced which further reduces the flux. It can also be seen that beyond a certain critical value, the shunt generator shows a reversal in trend of current values with decreasing voltages. This point of maximum current output is known as the breakdown point. At the short circuit condition, the only flux available to produce current is the residual magnetism of the armature.
To build up the voltage on a series generator, the external circuit must be connected and its resistance reduced to a comparatively low value. Since the armature is in series with the field, load current must be flowing to obtain flux in the field. As the voltage and current rise the load resistance may be increased to its normal value. As the external characteristic curve shows, the voltage output starts at zero, reaches a peak, and then falls back to zero.
The combination of a shunt field and a series field gives the best external characteristic as illustrated in Figure 24. The voltage drop, which occurs in the shunt machine, is compensated for by the voltage rise, which occurs in the series machine. The addition of a sufficient number of series turns offsets the armature IR drop and armature reaction effect, resulting in a flat-compound generator, which has a nearly constant voltage. If more series turns are added, the voltage may rise with load and the machine is known as an over-compound generator.
Voltage Regulation
Voltage Regulation is the change in terminal voltage with the change in load current at constant speed. A generator has good regulation if the change in voltage between no load and full load is small. If the change is large, the regulation is poor. Expressed in equation form:
Percent Voltage Regulation = (ENL - EFL ) / EFL x 100 or for some compound machines, Percent Voltage Regulation = (EFL - ENL ) / EFL x 100
Figure 24 shows that the regulation of a separately excited machine is better than that of a shunt machine. However, the best regulation is obtained with a compound machine. The series machine has practically no regulation at all and, therefore, has little practical application.
Motor Characteristics
Motor OperationAs previously stated, a conductor moving through a magnetic field due to the motor action also generates a voltage which is in opposition to the applied voltage. This is the back EMF. Then for motor action the voltage equation is:
V = E + IA RA = K1  S + IA RA S + IA RA |
| V = applied or terminal voltage | |
| E = back EMF | |
| IA = armature current | |
| RA = armature circuit resistance's | |
| K1 = machine constants | |
 = flux per pole = flux per pole | |
| S = speed |
The back or counter EMF acts as a control for the amount of current needed for each mechanical load. When the mechanical load is increased, the first effect is a reduction in speed. But a reduction in speed also causes a reduction in back EMF, thus making available an increased voltage for current flow in the armature. Therefore, the current increases which in turn increases the torque. Because of this action, a very slight decrease in speed is sufficient to meet the increased torque demand. Also, the input power is regulated to the amount required for supplying the motor losses and output.
Speed Torque Curves
Speed torque curves for the three forms of excitation are shown in Figure 25. In a shunt excited motor, the change in speed is slight and, therefore, it is considered a constant speed motor. Also, the field flux is nearly constant in a shunt motor and the torque varies almost directly with armature current.
In a series motor the drop in speed with increased torque is much greater. This is due to the fact that the field flux increases with increased current, thus tending to prevent the reduction in back EMF that is being caused by the reduction in speed. The field flux varies in a series motor and the torque varies as the square of the armature current until saturation is reached. Upon reaching saturation, the curve tends to approach the straight line trend of the shunt motor. The no load speed of a series motor is usually too high for safety and, therefore, it should never be operated without sufficient load.
A compound motor has a speed torque characteristic which lies between a shunt and series motor.
Speed Regulation
Speed regulation is the change in speed with the change in load torque, other conditions being constant. A motor has good regulation if the change between the no load speed and full load speed is small.
Percent Speed Regulation = (SNL - SFL) / SFL x 100 A shunt motor has good speed regulation while a series motor has poor speed regulation. For some applications such as cranes or hoists, the series motor has an advantage since it results in the more deliberate movement of heavier loads. Also, the slowing down of the series motor is better for heavy starting loads. However, for many applications the shunt motor is preferred.
Motor Starting
When the armature is not rotating, the back EMF is zero and the total applied voltage is available for sending current through the armature. Since the armature resistance is low, an enormous current would flow if voltage were applied under this condition. Therefore, it is necessary to insert an additional resistance in series with the armature until a satisfactory speed is reached where the back EMF will take over to limit the current input.
Losses And Efficiency
Friction and WindageThese losses include bearing friction, brush friction, and windage. They are also known as mechanical losses. They are constant at a given speed but vary with changes in speed. Power losses due to friction increase as the square of the speed and those due to windage increase as the cube of the speed.
Armature Copper Losses
These are the I2 R losses of the armature circuit, which includes the armature winding, commutator, and brushes. They vary directly with the resistance and as the square of the currents.
Field Copper Losses
These are the I2 R losses of the field circuit which can include the shunt field winding, series field winding, interpole windings and any shunts used in connection with these windings. They vary directly with the resistance and as the square of the currents.
Core Losses
These are the hysteresis and eddy current losses in the armature. With the continual change of direction of flux in the armature iron, an expenditure of energy is required to carry the iron through a complete hysteresis loop. This is the hysteresis loss. Also since the iron is a conductor and revolving in a magnetic field, a voltage will be generated. This, in turn, will result in small circulating currents known as eddy currents. If a solid core were used for the armature, the eddy current losses would be high. They are reduced by using thin laminations, which are insulated from each other. Hysteresis and eddy current losses vary with flux density and speed.
Efficiency
For generations or motors, the efficiency is equal to the output divided by the input. However, in a generator, the input is mechanical while the output is electrical. In a motor the opposite is true, therefore:
| Motor Efficiency = (Input - Losses) / Input | |
| Generator Efficiency = Output / (Output + Losses) |
Section 3: Horsepower Basics
In 18th century England, coal was feeding the industrial revolution and Thomas Newcomen invented a steam driven engine that was used to pump water from coal mines. It was a Scott however, by the name of James Watt, who in 1769 improved the steam engine making it truly workable and practical. In his attempt to sell his new steam engines, the first question coal mine owners asked was "can your engine out work one of my horses?" Watt didn't know since he didn't know how much work a horse could do. To find out, Watt and his partner bought a few average size horses and measured their work. They found that the average horse worked at the rate of 22,000 foot pounds per minute. Watt decided, for some unknown reason, to add 50% to this figure and rate the average horse at 33,000 foot pounds per minute.What's important is that there is now a system in place for measuring the rate of doing work. And there is a unit of power, horsepower.
If steam engines had been developed some place else in the world, where the horse was not the beast of burden, we might be rating motors in oxen power or camel power. Today, motors are also rated in Watts output.
| hp = lb x fpm / 33,000 | |
| hp = ft-lb x rpm / 5,252 | |
| kW = hp x 0.7457 | |
| hpMetric = hp x 1.0138 |
Horsepower and Electric Motors
| Torque = force x radius = lb x ft = T | |
| Speed = rpm = N | |
| Constant = 5252 = C | |
| HP = T x N / C |
T = k  Ia Ia |
D2 L and Torque
| 258AT = 324 D2 L | |
| 259AT = 378 D2 L |
 and 17% more Torque. Motor torque increases with an increase in iron and copper, combined with current. It can then be said that it takes iron and copper to produce torque and torque makes products. Or to put it another way, what you purchase to make product is TORQUE and that is IRON and COPPER. The rate of doing work is power and HORSEPOWER is a unit of power.
and 17% more Torque. Motor torque increases with an increase in iron and copper, combined with current. It can then be said that it takes iron and copper to produce torque and torque makes products. Or to put it another way, what you purchase to make product is TORQUE and that is IRON and COPPER. The rate of doing work is power and HORSEPOWER is a unit of power. Speed and DC Motors
Shunt wound DC motors
With motor load, temperature and field current held constant, speed is controlled by armature voltage.
E = ((Z / a) x  x P x (N / 60) x 10-8 ) + (I Ra + I Rip + I Rb ) x P x (N / 60) x 10-8 ) + (I Ra + I Rip + I Rb ) |
| N = (E - IR) / K |
 armature circuit resistance hot, 0.206
armature circuit resistance hot, 0.206  armature circuit resistance cold
armature circuit resistance cold Edrop = IR = 85 amp x 0.432  = 36.72 volts = 36.72 volts | |||
| 500 v arm - 36.72 v drop = 463.28 working volts | |||
| Volts per rpm = 463.28 / 1150 rpm = 0.40285 | |||
| Nbase speed = 1150 rpm = (500 v - 36.72 v) / 0.40285 | |||
| With 250 v on the armature, there is 213.28 working volts (250 - 36.72) | |||
| 213.28 / 0.40285 = 529 rpm (not 1/2 speed, 575 rpm) | |||
| N = 529 rpm = (250 v - 36.72 v) / 0.40285 | |||
| N = (E - IR) / K = (E - IR) / 0.40285 | |||
| K changes with changes in load and temperature | |||
| HPMetric = HP x 1.0138 | |||
| kW = HP x 0.7457 | |||
DC generator theory
Generators used in battery-charging systems must be regulated so as to not overcharge the battery(ies) they are connected to. Here is a crude, relay-based voltage regulator for a DC generator:

Simple electromechanical relay circuits such as this one were very common in automotive electrical systems during the 1950's, 1960's, and 1970's. The fundamental principle upon which their operation is based is called negative feedback: where a system takes action to oppose any change in a certain variable. In this case, the variable is generator output voltage. Explain how the relay works to prevent the generator from overcharging the battery with excessive voltage.

Simple electromechanical relay circuits such as this one were very common in automotive electrical systems during the 1950's, 1960's, and 1970's. The fundamental principle upon which their operation is based is called negative feedback: where a system takes action to oppose any change in a certain variable. In this case, the variable is generator output voltage. Explain how the relay works to prevent the generator from overcharging the battery with excessive voltage.
If the battery voltage becomes excessive, the relay opens and de-energizes the field winding. When the voltages sags back down to an acceptable level, the relay re-closes and re-energizes the field winding so that the generator can begin generating voltage again.
Challenge question: what would we have to change in this circuit to alter the generator's voltage regulation set-point (the "target" voltage at which the generator's output is supposed to be regulated)?
Challenge question: what would we have to change in this circuit to alter the generator's voltage regulation set-point (the "target" voltage at which the generator's output is supposed to be regulated)?
Notes:
The circuit drawn here is very similar to real generator regulator circuits used in American automobiles before the advent of inexpensive, reliable semiconductor circuits. I show it here not just for historical background, but also to demonstrate how relatively crude circuits are still able to perform certain tasks reasonably well.
"Negative feedback" is one of the fundamental principles of electronics and electrical engineering. A simple system like this provides a good way to gently introduce students to this vital concept.
The circuit drawn here is very similar to real generator regulator circuits used in American automobiles before the advent of inexpensive, reliable semiconductor circuits. I show it here not just for historical background, but also to demonstrate how relatively crude circuits are still able to perform certain tasks reasonably well.
"Negative feedback" is one of the fundamental principles of electronics and electrical engineering. A simple system like this provides a good way to gently introduce students to this vital concept.
Question 2:
A mechanic has an idea for upgrading the electrical system in an automobile originally designed for 6 volt operation. He wants to upgrade the 6 volt headlights, starter motor, battery, etc, to 12 volts, but wishes to retain the original 6-volt generator and regulator. Shown here is the original 6-volt electrical system:

The mechanic's plan is to replace all the 6-volt loads with 12-volt loads, and use two 6-volt batteries connected in series, with the original (6-volt) regulator sensing voltage across only one of those batteries:

Explain how this system is supposed to work. Do you think the mechanic's plan is practical, or are there any problems with it?
So long as the generator is capable of outputting 12 volts, this system will work!
Challenge question: identify factors that may prevent the generator from outputting enough voltage with the regulator connected as shown in the last diagram.
As a challenge for your students, ask them how well they think this system would work. It is a bit more complex than the system shown in the question, due to the two different load banks.
Challenge question: identify factors that may prevent the generator from outputting enough voltage with the regulator connected as shown in the last diagram.
Notes:
In this question, we see a foreshadowing of op-amp theory, with the regulator's negative feedback applied to what is essentially a voltage divider (two equal-voltage batteries being charged by the generator). The regulator circuit senses only 6 volts, but the generator outputs 12 volts.
Fundamentally, the focus of this question is negative feedback and one of its many practical applications in electrical engineering. The depth to which you discuss this concept will vary according to the students' readiness, but it is something you should at least mention during discussion on this question.
This idea actually came from one of the readers of my textbook series Lessons In Electric Circuits. He was trying to upgrade a vehicle from 12 volts to 24 volts, but the principle is the same. An important difference in his plan was that he was still planning on having some 12-volt loads in the vehicle (dashboard gauges, starter solenoid, etc.), with the full 24 volts supplying only the high-power loads (such as the starter motor itself):

In this question, we see a foreshadowing of op-amp theory, with the regulator's negative feedback applied to what is essentially a voltage divider (two equal-voltage batteries being charged by the generator). The regulator circuit senses only 6 volts, but the generator outputs 12 volts.
Fundamentally, the focus of this question is negative feedback and one of its many practical applications in electrical engineering. The depth to which you discuss this concept will vary according to the students' readiness, but it is something you should at least mention during discussion on this question.
This idea actually came from one of the readers of my textbook series Lessons In Electric Circuits. He was trying to upgrade a vehicle from 12 volts to 24 volts, but the principle is the same. An important difference in his plan was that he was still planning on having some 12-volt loads in the vehicle (dashboard gauges, starter solenoid, etc.), with the full 24 volts supplying only the high-power loads (such as the starter motor itself):

As a challenge for your students, ask them how well they think this system would work. It is a bit more complex than the system shown in the question, due to the two different load banks.
Question 3:
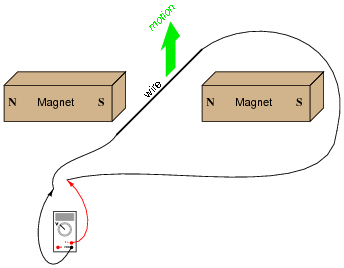
If an electric current is passed through this wire, which direction will the wire be pushed (by the interaction of the magnetic fields)?

Is this an example of an electric motor or an electric generator?
The wire will be pushed up in this motor example.
Notes:
A visual aid to understanding the interaction of the two magnetic fields is a diagram showing the lines of flux emanating from the permanent magnets, against the circular lines of flux around the wire. Ask those students who came across similar illustrations in their research to draw a picture of this on the board in front of the class, for those who have not seen it.
A visual aid to understanding the interaction of the two magnetic fields is a diagram showing the lines of flux emanating from the permanent magnets, against the circular lines of flux around the wire. Ask those students who came across similar illustrations in their research to draw a picture of this on the board in front of the class, for those who have not seen it.
Question 4:
If this wire (between the magnet poles) is moved in an upward direction, what polarity of voltage will the meter indicate?
Describe the factors influencing the magnitude of the voltage induced by motion, and determine whether this is an example of an electric motor or an electric generator.
The voltmeter will indicate a negative voltage in this generator example.
Notes:
Ask your students to explain their answers regarding factors that influence voltage magnitude. Where did they obtain their information? Are there any mathematical formulae relating these factors to induced voltage?
Ask your students to explain their answers regarding factors that influence voltage magnitude. Where did they obtain their information? Are there any mathematical formulae relating these factors to induced voltage?
Question 5:
If this wire (between the magnet poles) is moved in an upward direction, and the wire ends are connected to a resistive load, which way will current go through the wire?

We know that current moving through a wire will create a magnetic field, and that this magnetic field will produce a reaction force against the static magnetic fields coming from the two permanent magnets. Which direction will this reaction force push the current-carrying wire? How does the direction of this force relate to the direction of the wire's motion? Does this phenomenon relate to any principle of electromagnetism you've learned so far?
The reaction force will be directly opposed to the direction of motion, as described by Lenz's Law.
Follow-up question: What does this phenomenon indicate to us about the ease of moving a generator mechanism under load, versus unloaded? What effect does placing an electrical load on the output terminals of a generator have on the mechanical effort needed to turn the generator?
Follow-up question: What does this phenomenon indicate to us about the ease of moving a generator mechanism under load, versus unloaded? What effect does placing an electrical load on the output terminals of a generator have on the mechanical effort needed to turn the generator?
Notes:
If you happen to have a large, permanent magnet DC motor available in your classroom, you may easily demonstrate this principle for your students. Just have them spin the shaft of the motor (generator) with their hands, with the power terminals open versus shorted together. Your students will notice a huge difference in the ease of turning between these two states.
After your students have had the opportunity to discuss this phenomenon and/or experience it themselves, ask them why electromechanical meter movement manufacturers usually ship meters with a shorting wire connecting the two meter terminals together. In what way does a PMMC meter movement resemble an electric generator? How does shorting the terminals together help to protect against damage from physical vibration during shipping?
Ask your students to describe what factors influence the magnitude of this reaction force.
If you happen to have a large, permanent magnet DC motor available in your classroom, you may easily demonstrate this principle for your students. Just have them spin the shaft of the motor (generator) with their hands, with the power terminals open versus shorted together. Your students will notice a huge difference in the ease of turning between these two states.
After your students have had the opportunity to discuss this phenomenon and/or experience it themselves, ask them why electromechanical meter movement manufacturers usually ship meters with a shorting wire connecting the two meter terminals together. In what way does a PMMC meter movement resemble an electric generator? How does shorting the terminals together help to protect against damage from physical vibration during shipping?
Ask your students to describe what factors influence the magnitude of this reaction force.
Question 6:
Determine the polarity of induced voltage between the ends of this wire loop, as it is rotated between the two magnets:


Challenge question: if a resistor were connected between the ends of this wire loop, would it ßee" direct current (DC), or alternating current (AC)?
Notes:
Note that the two wire ends switch polarity as the loop rotates. Ask your students to explain why the polarities are as they are.
Note that the two wire ends switch polarity as the loop rotates. Ask your students to explain why the polarities are as they are.
Question 7:
If the ends of a wire loop are attached to two half-circular metal strips, arranged so that the two strips almost form a complete circle, and those strips are contacted by two "brushes" which connect to opposite poles of a battery, what polarity of voltage will be measured as the loop is rotated counter-clockwise?


Follow-up question: does the polarity measured at the two carbon brushes ever reverse? Or, to phrase the question another way, if a resistor were connected between the two brush contacts, would it ßee" direct current (DC) or alternating current (AC)? Explain your answer.
Notes:
Ask your students what the two half-circle metal strips are called, in electric motor/generator terminology.
Ask your students what the two half-circle metal strips are called, in electric motor/generator terminology.
Question 8:
How does Faraday's Law of electromagnetic induction relate to the voltage output of a DC generator? According to Faraday's Law, what factors can we alter to increase the voltage output by a DC generator?
Increase the [(dφ)/dt] rate of change, or increase the number of turns in the armature winding.
Notes:
Ask your students to write the equation for Faraday's Law on the whiteboard, and then analyze it in a qualitative sense (with variables increasing or decreasing in value) to validate the answers.
The first answer to this question (increase [(dφ)/dt]) has been left purposefully vague, in order to make students think. What, specifically, must be changed in order to increase this rate-of-change over time? Which real-world variables are changeable after the generator has been manufactured, and which are not?
Ask your students to write the equation for Faraday's Law on the whiteboard, and then analyze it in a qualitative sense (with variables increasing or decreasing in value) to validate the answers.
The first answer to this question (increase [(dφ)/dt]) has been left purposefully vague, in order to make students think. What, specifically, must be changed in order to increase this rate-of-change over time? Which real-world variables are changeable after the generator has been manufactured, and which are not?
Question 9:
DC generators will act as DC motors if connected to a DC power source and not spun at a sufficient speed. This is a problem in DC power systems, as the generator will act as a load, drawing energy from the battery, when the engine or other "prime mover" device stops moving. This simple generator/battery circuit, for example, would not be practical for this reason:

Back in the days when automobiles used DC generators to charge their batteries, a special relay called the reverse current cutout relay was necessary to prevent battery discharge through the generator whenever the engine was shut off:

When the generator is spun fast enough, it generates enough voltage to energize the shunt coil with enough current to close the relay contact. This connects the generator with the battery, and charging current flows through the series coil, creating even more magnetic attraction to hold the relay contact closed. If the battery reaches a full charge and does not draw any more charging current from the generator, the relay will still remain closed because the shunt coil is still energized.
However, the relay contact will open if the generator ever begins to act as a load to the battery, drawing any current from it. Explain why this happens.
If a reverse current goes through the series coil, the magnetic field produced will "buck" the magnetic field produced by the shunt coil, thus weakening the total magnetic field strength pulling at the armature of the relay.
Notes:
A "reverse current cutout" relay ingeniously exploits reversible magnetic polarities to close or open a contact under the proper conditions. Although DC generators are no longer used in the majority of automobile electrical systems (AC alternators using bridge rectifiers to convert AC to DC are used instead, with the rectifier circuit naturally preventing reverse current), this application provides an excellent opportunity to explore an application of relay technology in the context of generator control.
A "reverse current cutout" relay ingeniously exploits reversible magnetic polarities to close or open a contact under the proper conditions. Although DC generators are no longer used in the majority of automobile electrical systems (AC alternators using bridge rectifiers to convert AC to DC are used instead, with the rectifier circuit naturally preventing reverse current), this application provides an excellent opportunity to explore an application of relay technology in the context of generator control.
Question 10:
A shunt-wound generator has an electromagnet "field" winding providing the stationary magnetic field in which the armature rotates:

Like all electromagnets, the magnetic field strength produced is in direct proportion to the amount of current through the wire coil. But when the generator is sitting still, its output voltage is zero, and therefore there will be no current through the field winding to energize it and produce a magnetic field for the armature to rotate through. This causes a problem, since the armature will not have any voltage induced in its windings until it is rotating and it has a stationary magnetic field from the field winding to rotate through.
It seems like we have a catch-22 situation here: the generator cannot output a voltage until its field winding is energized, but its field winding will not be energized until the generator (armature) outputs some voltage. How can this generator ever begin to output voltage, given this predicament?
Usually, there is enough residual magnetism left in the field poles to initiate some generator action when turned.
Challenge question: what we could do if the generator's field poles ever totally lost their residual magnetism? How could the generator ever be started?
Challenge question: what we could do if the generator's field poles ever totally lost their residual magnetism? How could the generator ever be started?
Notes:
Back in the days when generators were common in automotive electrical systems, this used to be a fairly common problem. However, generators could be "flashed" so as to re-establish this residual magnetic field once again.
Back in the days when generators were common in automotive electrical systems, this used to be a fairly common problem. However, generators could be "flashed" so as to re-establish this residual magnetic field once again.
Question 11:
In a shunt-wound DC generator, the output voltage is determined by the rotational speed of the armature and the density of the stationary magnetic field flux. For a given armature speed, what prevents the output voltage from "running away" to infinite levels, since the output voltage energizes the field winding, which leads to greater field flux, which leads to greater output voltage, which leads to greater field flux, which leads to . . . ?

Obviously, there must be some inherent limit to this otherwise vicious cycle. Otherwise, the output voltage of a shunt-wound DC generator would be completely unstable.
At a certain amount of field winding current, the generator's field poles saturate, preventing further increases in magnetic flux.
Notes:
This question provides a great opportunity to review the concept of magnetic ßaturation," as well as introduce the engineering concept of positive feedback.
This question provides a great opportunity to review the concept of magnetic ßaturation," as well as introduce the engineering concept of positive feedback.
Question 12:
With regard to a DC electric generator, what is the neutral plane? Why is this important?
The "neutral plane" is that point of rotation where a rotating armature winding has no induced voltage in it, due to [(dφ)/dt] being equal to zero. In a simple, two-pole machine, the neutral plane is perpendicular to the centerline of the field poles:


Notes:
Ask your students why the "neutral plane" is an important aspect of a DC generator or motor's geometry. What relation does the neutral plane have with regard to brush positioning? At what point in the armature's rotation do we want to have the brushes break contact with one commutator bar and make contact with another: when the coil primary to that commutator segment is outputting maximum voltage, or minimum voltage?
Ask your students why the "neutral plane" is an important aspect of a DC generator or motor's geometry. What relation does the neutral plane have with regard to brush positioning? At what point in the armature's rotation do we want to have the brushes break contact with one commutator bar and make contact with another: when the coil primary to that commutator segment is outputting maximum voltage, or minimum voltage?
Question 13:
Suppose a generator is mechanically coupled to an internal combustion engine in an automobile, for the purpose of charging the starting battery. In order that the battery not be over-charged by the generator, there must be some way of controlling the generator's output voltage over a wide range of engine speeds.
How is this regulation of generator output voltage typically achieved? What variable within the generator may be most easily adjusted to maintain a nearly constant output voltage? Express your answer in relation to Faraday's Law of electromagnetic induction.
The most common method of generator voltage control is adjustment of field winding excitation.
Notes:
Although adjustable field winding excitation is the most popular form of generator output voltage control, it is not the only means. Challenge your students with inventing other means of charge control for the battery in this automotive electrical system, besides field winding excitation control. What else can we do to the generator, or to the circuit it is within, to achieve charge control for the battery?
Although adjustable field winding excitation is the most popular form of generator output voltage control, it is not the only means. Challenge your students with inventing other means of charge control for the battery in this automotive electrical system, besides field winding excitation control. What else can we do to the generator, or to the circuit it is within, to achieve charge control for the battery?
Question 14:
In most high-power DC generator and motor designs, the wire used to make the field winding is much thinner gauge than the wire used to make the armature winding. This indicates the relative magnitude of current through these respective windings, with the armature coils conducting much more current than the field coils.
That the armature conducts more current than the field is no small matter, because all current through the armature must be conducted through the brushes and commutator bars. The more current these components have to carry, the shorter their life, all other factors being equal.
Couldn't the generator be re-designed so that the field conducted most of the current, with the armature only conducting a small amount? This way, the brushes and commutator bars would only have to carry a fraction of their normal current, making them less expensive and longer-lived. Explain why this is impossible to do.
Hint: consider the design of a permanent-magnet generator.

No comments:
Post a Comment